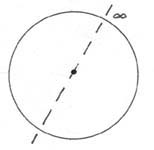
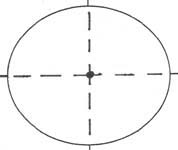
THE NEW SHORTER OXFORD ENGLISH DICTIONARY provides this definition of symmetry: "A specifically exact correspondence, in relative position, size, and shape of the parts of something with respect to a central point or one or more dividing lines or planes; a structure exhibiting this." This definition can be represented graphically by the following figures: The "something" on the left is a circle with infinitely many "dividing lines or planes" (but only one is shown). On the right is an ellipse, with two "dividing lines or planes", which are this figure's major and minor axes.


If one were to fold the circle on any diameter the resulting two hemispheres would be congruent, and therewith demonstrate symmetry of shape. Fold the ellipse on either axis and the two resulting semi-ellipses will also be congruent; thus, the ellipse is also a shape that is symmetrical. Many other geometric shapes can be similarly tested and will also be found to have this attribute of symmetry. In fact, it is difficult to find shapes in American cut glass that are not symmetrical -- but for an exception see Straus shape no. 313.
Thus far we have dealt with regular geometric shapes. One might assume, intuitively, that irregular shapes would lack symmetry. But, as illustrated by the following examples, this is not necessarily true:

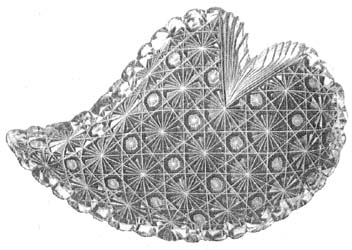
The maple-leaf bon-bon dish on the left has an irregular shape, yet, as indicated by the dashed line, the shape can be folded into two congruent parts and is, therefore, symmetrical. On the other hand, the more regularly shaped leaf on the right can not be divided in this manner. Therefore, its shape is asymmetrical. These two examples have been taken from the DORFLINGER composite catalog which was assembled and printed by the ACGA in 1997. (Incidentally, the leaf on the right is identified as shape no. 433 in both the Dorflinger catalog and in the Hawkes [Shape] Number Book, an unusual situation.)
Patterns can be analyzed in a similar manner. Geometric patterns, like shapes, are much more likely to be symmetrical than asymmetrical. However, some patterns that contain subdivided diamonds -- such as those in Dorflinger's Royal pattern --, swirl-type patterns, and almost all patterns that contain pinwheels, are asymmetrical. The motifs in the first and last of these patterns are also dimorphic. This characteristic, minor and often overlooked, is discussed in detail in the Royal pattern's file (see the dorflinger8.htm file in Part 2).
For a pinwheel pattern to be symmetrical it must have both clockwise- and counterclockwise-turning pinwheels. This is a rare occurrence, but examples can be found. Compare Clark's Corot pattern: "A panel of chair diamond [i.e., cane] is surrounded by a symmetrical arrangement of prism cutting and buzz stars [i.e., pinwheels]". Clark uses a less restrictive definition of symmetry in this quote -- taken from the company's c1910 catalog -- than what is used here. Only celery tray no. 788 is seen to carry both clockwise- and counterclockwise-turning pinwheels and is, by our definition, truly symmetrical.
It is useful to test patterns for symmetry by placing a small mirror perpendicular to the vertical "dividing line". If the image in the mirror replicates the image on the other side of the "dividing line", then the pattern is symmetrical. But if any part of the reflected image is the reverse of the image on the other side of the "dividing line", the pattern in question is asymmetrical. It is also possible to have a pattern that is made up of symmetrical sub-patterns which, when combined in a certain way, result in an overall, complete pattern that is asymmetrical. Strange but true (see the Nehemiah Packwood file for an example).
While it is always assumed that the characteristic of symmetry applies to the horizontal dimension of a pattern -- arranged around "a central point or one or more dividing lines or planes" -- a pattern can also be symmetrical vertically, especially: (i) If it is one of the so-called "overall" patterns, such as Russian, hobnail, etc., or (ii) If it has been transformed. Transformation is discussed in connection with Hawkes' Brazilian and Portland patterns. A few other patterns, such as Hawkes' Princess I pattern, although horizontally asymmetrical, are actually symmetrical vertically and so need no transformation. (It is incidental that the Princess I pattern is also dimorphic.) To use the mirror test for vertical symmetry, the mirror is placed on the "dividing line" which is now horizontal. The desirability of vertical symmetry often comes into play when a horizontal pattern, symmetrical or asymmetrical, is adapted for use on a vertical object.
Shapes can trump over patterns, as in the example of the maple-leaf dish shown in this file. It is cut in Dorflinger's Parisian pattern which is, of course, symmetrical. Yet the leaf's shape has forced the pattern to be asymmetrical because the pattern's large, double-mitered star-like pattern has an even number of points that contain fans and strawberry (fine) diamonds alternately. They do not "match up" when the leaf is folded or when the mirror test is used. If the number of points were odd, the cutter would have had to use either fans or strawberry (fine) diamonds within all of the points to produce a pattern that is symmetrical.
In contrast to geometric patterns, realistic patterns are usually asymmetrical, due to the freer designs demanded by the naturalistic subjects. They are produced, for the most part, by engraving techniques. Balance, which has been defined as "General harmony between the parts of anything; especially in Art, etc., harmony of proportion and design" (THE NEW SHORTER OXFORD ENGLISH DICTIONARY), takes over from symmetry to provide a pleasant aesthetic experience: for example, three pears placed opposite a pair of apples on a tray; a carefully arranged bunch of grapes in the center of a plate; or a gadding vine artfully encircling a wine glass.
Most designers of shapes and geometric patterns have followed the dictates of symmetry. While asymmetry is not necessarily a negative factor in design -- a small amount can enliven a shape or pattern -- it must be used conservatively. Everyday objects, viewed every day, need to provide a sense of equilibrium -- that restful feeling that is produced by designs that are symmetrical. The patterns on most cut-glass objects provide this. As important as symmetry is, other factors must also be taken into account, when one evaluates the "worth" of shapes and patterns in American cut glass.
Updated 27 Apr 2004